Lecture 02-03 线性代数基础与线性变换

线性代数基础

• 叉乘计算公式（两个向量的叉积等价于一个矩阵与一个向量的乘积）

  

• 任意向量在三维坐标中的分解（该向量在三个基方向上的投影之和）

  

• 向量与矩阵的联系

  

线性变换

• 基本概念

  • 如果 $AA^T=E$（E 为单位矩阵）或 $A^TA=E$，则 n 阶实矩阵 A 称为正交矩阵
  • 设 A 是一个 n 阶矩阵，若存在另一个 n 阶矩阵 B，使得： $AB=BA=E$ ，则称方阵 A 可逆，并称方阵 B 是 A 的逆矩阵

• 齐次坐标的目的：将线性变换（压缩、旋转等）和非线性变换（平移）都用一个变换矩阵来表示。向量和点的区别：3D 向量的第 4 个代数分量是 0，而 3D 点的第 4 个代数分量是 1。

  
  

• 仿射变换，又称仿射映射，是指在几何中，一个向量空间进行一次线性变换并接上一个平移，变换为另一个向量空间。

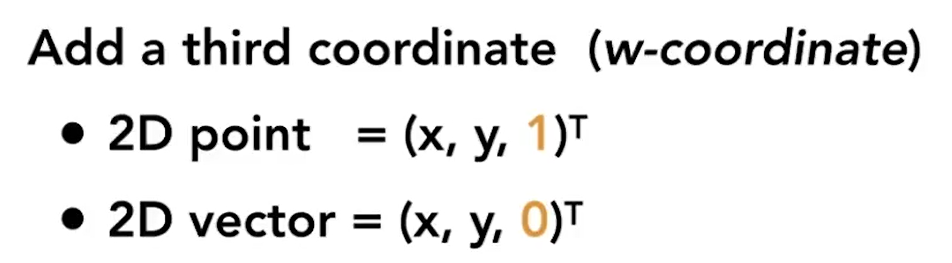
• 投影变换（projection transformation）是将一种地图投影点的坐标变换为另一种地图投影点的坐标的过程。研究投影点坐标变换的理论和方法。

• 从中可以思考得知，对于平移 T、旋转 R、缩放 S 这 3 个最常见的仿射变换，平移变换只对于点才有意义，因为普通向量没有位置概念，只有大小和方向
  

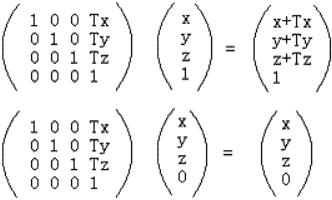
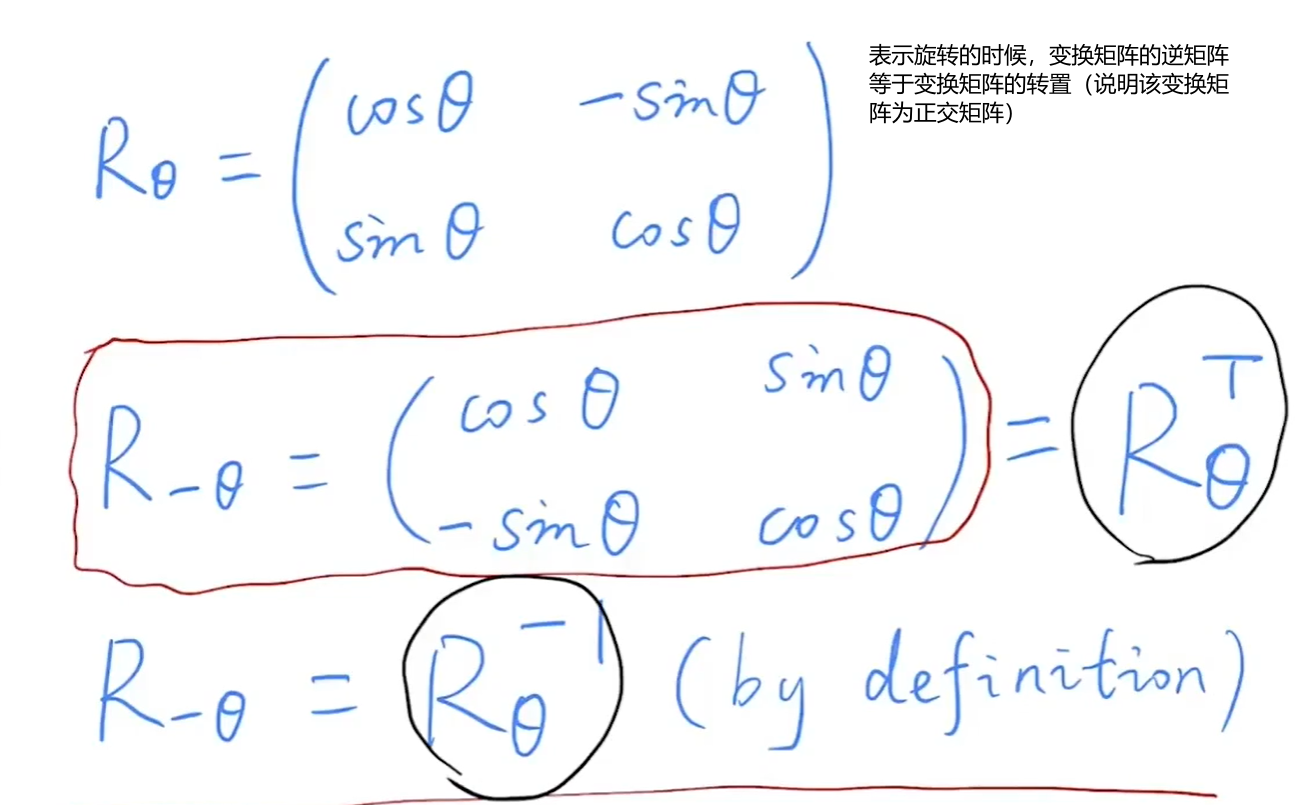
• 表示旋转的时候，变换矩阵的逆矩阵等于变换矩阵的转置（说明该变换矩阵为正交矩阵）

  

• 如何判断一个点是否在三角形中？
  
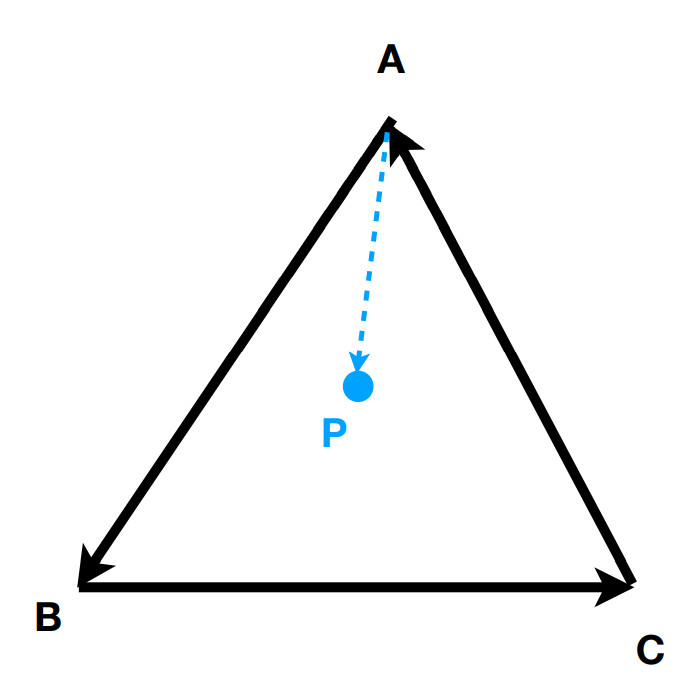
  按照逆时针方向连接三个顶点形成三个向量：$\vec{AB} \times\vec{AP}$、$\vec{BC}\times\vec{BP}$、$\vec{CA}\times\vec{CP}$，计算它们的结果是否同号（同为正或者同为负），是，则在三角形内部。